Trigonometry (IB SL)

1

(IB/s1/2017/November/Paper2/q10) [Maximum mark: 17] Note: In this question, distance is in millimetres. Let $f(x)=x+a \sin \left(x-\frac{\pi}{2}\right)+a$, for $x \geq 0$ (a) Show that $f(2 \pi)=2 \pi$. The graph of $f$ passes through the origin. Let $\mathrm{P}_{t}$ be any point on the graph of $f$ with $x$-coordinate $2 k \pi$, where $k \in \mathbb{N} .$ A straight line $L$ passes through all the points $\mathrm{P}_{k}$. (b) (i) Find the coordinates of $P_{0}$ and of $P_{1}$. (ii) Find the equation of $L$. (c) Show that the distance between the $x$-coordinates of $\mathrm{P}_{k}$ and $\mathrm{P}_{k+1}$ is $2 \pi$. Diagram 1 shows a saw. The length of the toothed edge is the distance $\mathrm{AB}$.

2

(Continue: 1) The toothed edge of the saw can be modelled using the graph of $f$ and the line $L$. Diagram 2 represents this model. The shaded part on the graph is called a tooth. A tooth is represented by the region enclosed by the graph of $f$ and the line $L$, between $\mathrm{P}_{t}$ and $\mathrm{P}_{z+1}^{-}$ (d) A saw has a toothed edge which is $300 \mathrm{~mm}$ long. Find the number of complete teeth on this saw.

3

(IB/s1/2017/May/paper2tz1/q7) [Maximum mark: 7] A particle $\mathrm{P}$ moves along a straight line. Its velocity $v_{\mathrm{p}} \mathrm{ms}^{-1}$ after $t$ seconds is given by $v_{\mathrm{P}}=\sqrt{t} \sin \left(\frac{\pi}{2} t\right)$, for $0 \leq t \leq 8 .$ The following diagram shows the graph of $v_{\mathrm{p}}$. (a) (i) Write down the first value of $t$ at which $\mathrm{P}$ changes direction. (ii) Find the total distance travelled by $\mathrm{P}$, for $0 \leq t \leq 8$. (b) A second particle $Q$ also moves along a straight line, Its velocity, $v_{Q} m s^{-1}$ after $t$ seconds is given by $v_{\mathrm{Q}}=\sqrt{t}$ for $0 \leq t \leq 8$. After $k$ seconds $Q$ has travelled the same total distance as P. Find $k$, [4]

4

(IB/s1/2017/May/paper2tz1/q8) [Maximum mark: 14] At Grande Anse Beach the height of the water in metres is modelled by the function $h(t)=p \cos (q \times t)+r$, where $t$ is the number of hours after $21: 00$ hours on 10 December 2017 . The following diagram shows the graph of $h$, for $0 \leq t \leq 72$. The point $\mathrm{A}(6.25,0.6)$ represents the first low tide and $\mathrm{B}(12.5,1.5)$ represents the next high tide. (a) (i) How much time is there between the first low tide and the next high tide? (ii) Find the difference in height between low tide and high tide. (b) Find the value of (i) $p$; (ii) $q$ : (iii) $r$. [7] (c) There are two high tides on 12 December 2017. At what time does the sccond high tide occur?

5

(IB/sl/2017/May/paper2tz2/q4) [Maximum mark: 6] The depth of water in a port is modelled by the function $d(t)=p \cos q t+7.5$, for $0 \leq t \leq 12$, where $t$ is the number of hours after high tide. At high tide, the depth is $9.7$ metres. At low tide, which is 7 hours later, the depth is $5.3$ metres. (a) Find the value of $p$. (b) Find the value of $q$. (c) Use the model to find the depth of the water 10 hours after high tide.

6

(IB/s1/2016/November/Paper2/q10) [Maximum mark: 15] The following diagram shows the graph of $f(x)=a \sin b x+c$, for $0 \leq x \leq 12$. The graph of $f$ has a minimum point at $(3,5)$ and a maximum point at $(9,17)$. (a) (i) Find the value of $c$. (ii) Show that $b=\frac{\pi}{6}$, (iii) Find the value of $a$. The graph of $g$ is obtained from the graph of $f$ by a translation of $\left(\begin{array}{l}k \\ 0\end{array}\right)$. The maximum point on the graph of $g$ has coordinates $(11.5,17)$. (b) (i) Write down the value of $k$. (ii) Find $g(x)$ The graph of $g$ changes from concave-up to concave-down when $x=w$. (c) (i) Find $w$. (ii) Hence or otherwise, find the maximum positive rate of change of $g$. $[6]$

7	(IB/s1/2016/May/paper1tz1/q3) [Maximum mark: 7] Let $f(x)=3 \sin \left(\frac{\pi}{2} x\right)$, for $0 \leq x \leq 4$. (a) (i) Write down the amplitude of $f$. (ii) Find the period of $f$. [3] (b) On the following grid sketch the graph of $f$. $[4]$

8

(IB/s1/2016/May/paper2tz1/q9) [Maximum mark: 14] A particle P moves along a straight line so that its velocity, $v \mathrm{~ms}^{-1}$, after $t$ seconds, is given by $r=\cos 3 t-2 \sin t-0.5$, for $0 \leq t \leq 5$. The initial displacement of P from a fixed point $O$ is 4 metres. (a) Find the displacement of $\mathrm{P}$ from $\mathrm{O}$ after 5 seconds. The following sketch shows the graph of $v$. (b) Find when $\mathrm{P}$ is first at rest. [2] (c) Write down the number of times $\mathrm{P}$ changes direction. (d) Find the acceleration of $\mathrm{P}$ after 3 seconds. (e) Find the maximum speed of $P$. [3]

9

(IB/sl/2016/May/paper2tz2/q4) [Maximum mark: 8] The height, $h$ metres, of a seat on a Ferris wheel after $t$ minutes is given by $$ h(t)=-15 \cos 1.2 t+17, \text { for } t \geq 0 $$ (a) Find the height of the seat when $t=0$. (b) The seat first reaches a height of $20 \mathrm{~m}$ after $k$ minutes. Find $k$. (c) Calculate the time needed for the seat to complete a full rotation, giving your answer correct to one decimal place.

10

(IB/sl/2019/May/paper1tz2/q7) [Maximum mark: 7] Consider the graph of the function $f(x)=2 \sin x, 0 \leq x < 2 \pi$. The graph of $f$ intersects the line $y=-1$ exactly twice, at point $\mathrm{A}$ and point $\mathrm{B}$. This is shown in the following diagram. (a) Find the $x$-coordinate of $\mathrm{A}$ and of $\mathrm{B}$. Consider the graph of $g(x)=2 \sin p x, 0 \leq x < 2 \pi$, where $p>0$. (b) Find the greatest value of $p$ such that the graph of $g$ does not intersect the line $y=-1$.

11	(IB/s1/2018/November/Paper1/q7) [Maximum mark: 6] Given that $\sin x=\frac{1}{3}$, where $0 < x < \frac{\pi}{2}$, find the value of $\cos 4 x$.

12

(IB/s1/2018/May/paper2tz1/q10) [Maximum mark: 15] Let $f(x)=12 \cos x-5 \sin x,-\pi \leq x \leq 2 \pi$, be a periodic function with $f(x)=f(x+2 \pi)$. The following diagram shows the graph of $f$. There is a maximum point at $\mathrm{A}$. The minimum value of $f$ is $-13$. (a) Find the coordinates of $\mathrm{A}$. (b) For the graph of $f$, write down (i) the amplitude; (ii) the period. (c) Hence, write $f(x)$ in the form $p \cos (x+r)$.

13

(IB/s1/2018/May/paper2tz1/q10b) A ball on a spring is attached to a fixed point $O$. The ball is then pulled down and released, so that it moves back and forth vertically. The distance, $d$ centimetres, of the centre of the ball from $\mathrm{O}$ at time $t$ seconds, is given by $$d(t)=f(t)+17,0 \leq t \leq 5$$ (d) Find the maximum speed of the ball. (e) Find the first time when the ball's speed is changing at a rate of $2 \mathrm{~cm} \mathrm{~s}^{-2}$. [5]

14

(IB/s1/2018/May/paper2tz2/q6) [Maximum mark: 8] At an amusement park, a Ferris wheel with diameter 111 metres rotates at a constant speed. The bottom of the wheel is $k$ metres above the ground. A seat starts at the bottom of the wheel. The wheel completes one revolution in 16 minutes. (a) After 8 minutes, the seat is $117 \mathrm{~m}$ above the ground. Find $k$. After $t$ minutes, the height of the seat above ground is given by $h(t)=61.5+a \cos \left(\frac{\pi}{8} t\right)$. for $0 \leq t \leq 32$, (b) Find the value of $a$. (c) Find when the seat is $30 \mathrm{~m}$ above the ground for the third time.

15	(IB/s1/2016/November/Paper1/q2) [Maximum mark: 5] Let $\sin \theta=\frac{\sqrt{5}}{3}$, where $\theta$ is acute. (a) Find $\cos \theta$. (b) Find $\cos 2 \theta$. [2]

16

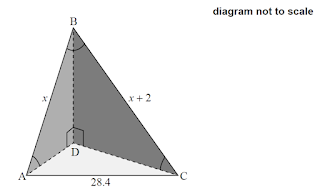
(IB/sl/2019/November/Paper2/q6) [Maximum mark: 6] The diagram below shows a triangular-based pyramid with base ADC. Edge $\mathrm{BD}$ is perpendicular to the edges $\mathrm{AD}$ and $\mathrm{CD}$. $\mathrm{AC}=28.4 \mathrm{~cm}, \mathrm{AB}=x \mathrm{~cm}, \mathrm{BC}=x+2 \mathrm{~cm}, \mathrm{ABC}=0.667, \mathrm{BAD}=0.611$ Calculate AD.

17	(IB/s1/2019/November/Paper1/q6) [Maximum mark: 8] Let $f(x)=4 \cos \left(\frac{x}{2}\right)+1$, for $0 \leq x \leq 6 \pi$. Find the values of $x$ for which $f(x)>2 \sqrt{2}+1$

18

(IB/sl/2019/May/paper1tz1/q3) [Maximum mark: 7] The following diagram shows a right triangle $\mathrm{ABC}$. Point $\mathrm{D}$ lies on $\mathrm{AB}$ such that $\mathrm{CD}$ bisects ACB. (a) Given that $\sin \theta=\frac{3}{5}$, find the value of $\cos \theta$. (b) Find the value of $\cos 2 \theta$. [2] (c) Hence or otherwise, find $\mathrm{BC}$. [2]

19

$(\mathrm{IB} / \mathrm{s} 1 / 2019 /$ May $/$ paper $2 \mathrm{tz} 2 / \mathrm{q} 3)$ [Maximum mark: 7] The following diagram shows the quadrilateral $\mathrm{ABCD}$. $\mathrm{AB}=6.73 \mathrm{~cm}, \mathrm{BC}=4.83 \mathrm{~cm}, \mathrm{BC} \mathrm{D}=78.2^{\circ}$ and $\mathrm{CD}=3.80 \mathrm{~cm}$ (a) Find BD. (b) The area of triangle $\mathrm{ABD}$ is $18.5 \mathrm{~cm}^{2}$. Find the possible values of $\theta$.

20

(IB/s1/2018/November/Paper2/q7) [Maximum mark: 6] A communication tower, $T$, produces a signal that can reach cellular phones within a radius of $32 \mathrm{~km}$. A straight road passes through the area covered by the tower's signal. The following diagram shows a line representing the road and a circle representing the area covered by the tower's signal. Point $R$ is on the circumference of the circle and points $S$ and $R$ are on the road. Point $\$$ is $38 \mathrm{~km}$ from the tower and RST $=43^{\circ}$, (a) Let SR $=x$. Use the cosine rule to show that $x^2-(76 \cos 43^{\circ})x+420=0.$ (b) Hence or otherwise, find the total distance along the road where the signal from the tower can reach cellular phones.

21	(IB/sl/2018/May/paper2tz1/q6) [Maximum mark: 7] Triangle $\mathrm{ABC}$ has $a=8.1 \mathrm{~cm}, b=12.3 \mathrm{~cm}$ and area $15 \mathrm{~cm}^{2}$. Find the largest possible perimeter of triangle $\mathrm{ABC}$.

22	(IB/s1/2018/May/paper2tz2/q2) [Maximum mark: 6] The following diagram shows quadrilateral $\mathrm{ABCD}$. $$\mathrm{AB}=11 \mathrm{~cm}, \mathrm{BC}=6 \mathrm{~cm}, \mathrm{BAD}=59^{\circ}, \mathrm{ADB}=100^{\circ} \text {, and } \mathrm{CBD}=82^{-}$$ (a) Find $\mathrm{DB}$. (b) Find DC.

23	(IB/s1/2017/November/Paper2/q1) [Maximum mark: 6] The following diagram shows a triangle $\mathrm{ABC}$. $$\mathrm{AB}=5 \mathrm{~cm}, \mathrm{CAB}=50^{\circ} \text { and } \mathrm{ACB}=112^{\circ}$$ (a) Find $\mathrm{BC}$. (b) Find the area of triangle $\mathrm{ABC}$.

24	$(\mathrm{IB} / \mathrm{sl} / 2017 /$ May $/$ paper $1 \mathrm{tz} 1 / \mathrm{q} 3)$ [Maximum mark; 6] The following diagram shows triangle $\mathrm{PQR}$. $$\mathrm{PQR}=30^{\circ}, \mathrm{QR} \mathrm{P}=45^{*} \text { and } \mathrm{PQ}=13 \mathrm{~cm} $$ Find PR.

25

(IB/sl/2017/May/paper2tz2/q9) [Maximum mark: 15] A ship is sailing north from a point $A$ towards point $D$. Point $C$ is $175 \mathrm{~km}$ north of $A$. Point $\mathrm{D}$ is $60 \mathrm{~km}$ north of $\mathrm{C}$. There is an island at $\mathrm{E}$. The bearing of $\mathrm{E}$ from $\mathrm{A}$ is 055 . The bearing of $\mathrm{E}$ from $\mathrm{C}$ is $134^{\prime \prime}$. This is shown in the following diagram. (a) Find the bearing of $\mathrm{A}$ from $\mathrm{E}$. (b) Find CE. (c) Find DE. (d) When the ship reaches $\mathrm{D}$, it changes direction and travels directly to the island at $50 \mathrm{~km}$ per hour. At the same time as the ship changes direction, a boat starts travelling to the island from a point $B$. This point $B$ lies on (AC), between A and C, and is the closest point to the island. The ship and the boat arrive at the island at the same time. Find the speed of the boat.

26

(IB/s1/2016/May/paper1tz1/q6) [Maximum mark: 7] The following diagram shows triangle $\mathrm{ABC}$. The point $\mathrm{D}$ lies on [BC] so that [AD] bisects BAC $AB= 2\sqrt 5$ cm, $AC=x$ cm, and $D\hat A C=\theta,$ where $\sin\theta=\frac 23.$ The area of triangle $\mathrm{ABC}$ is $5 \mathrm{~cm}^{2}$. Find the value of $x .$

27

(IB/s1/2016/May/paper2tz1/q3) [Maximum mark: 7 ] The following diagram shows three towns $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$. Town $\mathrm{B}$ is $5 \mathrm{~km}$ from Town $\mathrm{A}$, on a bearing of $070^{\circ}$. Town C is $8 \mathrm{~km}$ from Town B, on a bearing of $115^{\circ}$. (a) Find $\mathrm{ABC}$. (b) Find the distance from Town $\mathrm{A}$ to Town $\mathrm{C}$. (c) Use the sine rule to find $A \hat{C B}$.

28	(IB/s1/2016/May/paper2tz2/q2) [Maximum mark: 6] The following diagram shows a quadrilateral $\mathrm{ABCD}$. $\mathrm{AD}=7 \mathrm{~cm}, \mathrm{BC}=8 \mathrm{~cm}, \mathrm{CD}=12 \mathrm{~cm}, D\hat A B=1.75$ radians, $A\hat BD=0.82$ radians. (a) Find BD. [3] (b) Find $D\hat BC.$ [3]

29	(IB/s1/2015/May/paper1tz1/q5) [Maximum mark: 7 ] Given that $\sin x=\frac{3}{4}$, where $x$ is an obtuse angle, find the value of (a) $\cos x$; (b) $\cos 2 x$. [3]

30	(IB/sl/2015/May/paper1tz2/q2) [Maximum mark: 6] Let $f(x)=a \sin b x$, where $b>0 .$ The following diagram shows part of the graph of $f .$ (a) (i) Find the period of $f$. (ii) Write down the amplitude of $f$. (b) (i) Write down the value of $a$. (ii) Find the value of $b$. [3]

31

(IB/sl/2015/May/paper2tz1/q8) [Maximum mark: 13] The following diagram shows a straight shoreline, with a supply store at $\mathrm{S}$, a town at $\mathrm{T}$, and an island L. A boat delivers supplies to the island. The boat leaves $\mathrm{S}$, and sails to the island. Its path makes an angle of $20^{4}$ with the shoreline. (a) The boat sails at $6 \mathrm{~km}$ per hour, and arrives at $\mathrm{L}$ after $1.5$ hours. Find the distance from $S$ to $L$ It is decided to change the position of the supply store, so that its distance from $\mathrm{L}$ is $5 \mathrm{~km}$. The following diagram shows the two possible locations $\mathrm{P}$ and $\mathrm{Q}$ for the supply store. (b) Find the size of S\hat{P} L and of SÓL. (c) The town wants the new supply store to be as near as possible to the town. (i) State which of the points $\mathrm{P}$ or $\mathrm{Q}$ is chosen for the new supply store. (ii) Hence find the distance between the old supply store and the new one. [6]

32	(IB/s1/2015/May/paper2tz2/q1) [Maximum mark: 6] The following diagram shows triangle $\mathrm{ABC}$. $\mathrm{BC}=10 \mathrm{~cm}, \mathrm{ABC}=80^{\circ}$ and $\mathrm{BAC}=35^{\prime}$ (a) Find $\mathrm{AC}$. (b) Find the area of triangle $\mathrm{ABC}$.

33

(IB/sl/2015/November/Paper2/q8) [Maximum mark: 14] The following diagram shows the quadrilateral $\mathrm{ABCD}$. $\mathrm{AD}=6 \mathrm{~cm}, \mathrm{AB}=15 \mathrm{~cm}, \mathrm{ABC}=44^{\circ}, \mathrm{ACB}=83^{*}$ and $\mathrm{DAC}=\theta$ (a) Find $\mathrm{AC}$. (b) Find the area of triangle $\mathrm{ABC}$. The area of triangle $\mathrm{ACD}$ is half the area of triangle $\mathrm{ABC}$. (c) Find the possible values of $\theta$. (d) Given that $\theta$ is obtuse, find $\mathrm{CD}$. [3]

Answer (Trigo)

1 (a) Show (b)(i) $P_{0}=(0,0), P_{1}(2 \pi, 2 \pi)$ (ii) $y=x$ (c) Show 

2 (d) 33

3 (a) (i) $t=2$ (ii) $9.65$ (b) $k=5.94$

4 (a)(i) $6.25$ (ii) $0.9$ (b) (i) $p=0.45$ (ii) $q=\frac{4 \pi}{25}$  (iii) $r=1.05$ (d) $23: 00$

5 (a) $\quad p=2.2$ (b) $q=\frac{\pi}{7}$ (c) $7.01$

6 (a)(i) $\quad c=11$ (ii) $b=\frac{\pi}{6}$ (iii) $a=-6$ (b) (i) $k=2.5$ (ii) $g(x)=-6 \sin \left(\frac{\pi}{6}(x-2.5)\right)+11$ (c)(i) $w=8.5$ (ii) $\pi$

7 (a)(i) 3 (ii) 4 (b) Graph

8 (a) $0.284$ (b) $t=0.180$ (c) 2 (d) $0.744$ (e) $3.28$

9 (a) $h(0)=2$ (b) $k=1.48$ (c) $5.2$

10 (a) $x=\frac{7\pi}{6},\frac{11\pi}{6}$ (b) $ p=\frac{7}{12} $

11 $\frac{11}{81}$

12 (a) $A(-0.395,13)$ (b) (i) $13$ (ii) $2 \pi$ (c) $f(x)=13 \cos (x+0.395)$ 

13 (d) 13 (e) $1.02$

14 (a) $k=6$ (b) $a=-55.5$ (c) $t=18.5$

15 (a) $\quad \cos \theta=\frac{2}{3}$ (b) $\cos 2 \theta=-\frac{1}{9}$

16 34.6

17 $0\le x<\frac{\pi}{2}, \frac{7\pi}{2} <x<\frac{9\pi}{2}$

18 (a) $\frac{4}{5}$ (b) $\frac{7}{25}$ (c) 50

19 (a) $5.50$ (b) $\theta=92.0^{\circ}$ or $1.61$

20 (a) Show (b) $37.5$

21 perimeter $=40.6$

22 (a) $D B=9.57$ (b) $D C=10.6$

23 (a) $B C=4.13$ (b) Area $=3.19$

24 $P R=\frac{13 \sqrt{2}}{2}$

25 (a) $235$ (b) 146 (c) 193 (d) $27.3$

26 $x=\frac{9}{4}$

27 (a) $\quad A \hat{B} C=135^{\circ}$ (b) $12.1$ (c) $A\hat{ C} B=17.0^{\circ}$

28 (a) $B D=9.42$ (b) $B \widehat{D} C=1.51$

29(a) $\cos x=-\frac{\sqrt{7}}{4}$ (b) $\cos 2 x=-\frac{1}{8}$
30(a)(i) $\pi $ (ii) 3 (b) (i) $a=3$ (i) $b=2$
31(a) $9$ (b) $S\hat{ Q} L=142^{\circ}, \quad S \hat{P} L=38.0^{\circ}$ (c) (i) new store is at Q (ii) $4.52$
32(a) $A C=17.2$ (b) area $=77.8$
33(a) $\quad A C=10.5$ (b) area $=62.9$ (c) $\theta=86.7,93.3$ (d) $12.4$