$\def\D{\displaystyle}\def\frac{\dfrac}$
1 (CIE 2012, s, paper 12, question 10)
(a) It is given that $\D f(x) =\frac{1}{2+x}$ for $\D x \not= -2, x\in R.$
(i) Find $\ D f ″(x).$ [2]
(ii) Find $\D f^{-1} (x).$ [2]
(iii) Solve $\D f^2(x) = -1.$ [3]
(b) The functions g, h and k are defined, for $\D x\in R,$ by
$\D \begin{array}{rcl}g(x)&=&\frac{1}{x+5},x\not= -5\\h(x)&=&x^2-1,\\k(x)&=&2x+1.\end{array}$
Express the following in terms of g, h and/or k.
(i) $\D \frac{1}{(x^2-1)+5}$ [1]
(ii) $\D \frac{2}{x+5}+1$ [1]
2 (CIE 2012, s, paper 21, question 12or)
A function g is defined by $\D g : x \mapsto 5x^2 + px + 72,$ where $\D p$ is a constant. The function can also be written as $\D g : x \mapsto 5(x - 4)^2 + q.$
(i) Find the value of $\D p$ and of $\D q.$ [3]
(ii) Find the range of the function g. [1]
(iii) Sketch the graph of the function on the axes provided. [2]
(iv) Given that the function $\D h$ is defined by $\D h : x \mapsto \ln x,$ where $\D x > 0,$ solve the equation $\D gh(x) = 12.$ [4]
3 (CIE 2012, w, paper 11, question 9)
A function g is such that $\D g(x) = \frac{1}{2x-1}$ for $\D 1 \le x \le 3.$
(i) Find the range of $\D g.$ [1]
(ii) Find $\D g^{-1}(x).$ [2]
(iii) Write down the domain of $\D g^{-1}(x).$ [1]
(iv) Solve $\D g^2(x) = 3.$ [3]
4 (CIE 2012, w, paper 23, question 12either)
(i) Express $\D 4x^2 + 32x + 55$ in the form $\D (ax + b)^2 + c,$ where a, b and c are constants and a is
positive. [3]
The functions f and g are defined by
\begin{eqnarray*}f:x&\mapsto& 4x^2+32x+55 \mbox{ for } x>-4\\g:x&\mapsto&\frac{1}{x}\mbox{for }x>0.\end{eqnarray*}
(ii) Find $\D f^{-1}(x).$ [3]
(iii) Solve the equation $\D fg(x) = 135.$ [4]
5 (CIE 2012, w, paper 23, question 12or)
The functions h and k are defined by
\begin{eqnarray*}h:x&\mapsto& \sqrt{2x-7} \mbox{ for } x>c\\k:x&\mapsto&\frac{3x-4}{x-2}\mbox{ for }x>2.\end{eqnarray*}
(i) State the least possible value of c. [1]
(ii) Find $\D h^{-1}(x).$ [2]
(iii) Solve the equation $\D k(x) = x.$ [3]
(iv) Find an expression for the function $\D k^2,$ in the form $\D k^2 : x \mapsto a + \frac{b}{x}$ where a and b are constants. [4]
6 (CIE 2013, s, paper 21, question 11)
A one-one function f is defined by $\D f(x)= (x- 1)^2- 5 $ for $\D x \ge k .$
(i) State the least value that k can take. [1]
For this least value of k
(ii) write down the range of f, [1]
(iii) find $\D f^{-1}(x),$ [2]
(iv) sketch and label, on the axes below, the graph of $\D y = f(x)$ and of $\D y= f^{-1}(x),$ [2]
(v) find the value of x for which $\D f(x)= f^{-1}(x).$ [2]
7 (CIE 2013, w, paper 11, question 12)
(a) A function f is such that $\D f (x)= 3x^2- 1$ for $\D - 10 \le x \le 8.$
(i) Find the range of f. [3]
(ii) Write down a suitable domain for f for which $f^{-1}$ exists. [1]
(b) Functions g and h are defined by
$\D g(x)= 4e^x- 2$ for $\D x \in R,$
$h(x) = \ln 5x$ for $\D x > 0.$
(i) Find $\D g^{-1} (x).$ [2]
(ii) Solve $\D gh(x) = 18.$ [3]
8 (CIE 2013, w, paper 13, question 5)
For $\D x\in R,$ the functions f and g are defined by
\begin{eqnarray*}f(x)&=&2x^3,\\g(x)&=&4x-5x^2.\end{eqnarray*}
(i) Express $\D f^2\left(\frac{1}{2}\right)$ as a power of 2. [2]
(ii) Find the values of x for which f and g are increasing at the same rate with respect to x. [4]
9 (CIE 2014, s, paper 21, question 12)
The functions f and g are defined by
\begin{eqnarray*}f(x)&=&\frac{2x}{x+1}\mbox{ for } x>0,\\g(x)&=&\sqrt{x+1}\mbox{ for } x>-1.\end{eqnarray*}
(i) Find $\D fg(8)$. [2]
(ii) Find an expression for $\D f^2(x),$ giving your answer in the form $\D \frac{ax}{bx+c},$ where a, b and c are integer to be found. [3]
(iii) Find an expression for $\D g^{-1}(x),$ stating its domain and range. [4]
(iv) On the same axes, sketch the graphs of $\D y=g(x)$ and $\D y=g^{-1}(x),$ indicating the geometrical relationship between the graphs. [3]
10 (CIE 2014, s, paper 22, question 11)
The functions f and g are defined, for real values of x greater than 2, by
\begin{eqnarray*}f(x)&=&2^x-1,\\g(x)&=&x(x+1).\end{eqnarray*}
(i) State the range of f. [1]
(ii) Find an expression for $\D f^{-1} (x),$ stating its domain and range. [4]
(iii) Find an expression for $\D gf (x)$ and explain why the equation $\D gf (x) = 0$ has no solutions. [4]
11 (CIE 2014, s, paper 23, question 12)
The function f is such that $\D f(x) = \sqrt{x-3}$ for $\D 4\le x\le 28.$
(i) Find the range of f. [2]
(ii) Find $\D f^2 (12).$ [2]
(iii) Find an expression for $\D f^{-1} (x).$ [2]
The function g is defined by $\D g(x)=\frac{120}{x}$ for $\D x\ge 0.$
(iv) Find the value of x for which $\D gf (x) = 20.$ [3]
12 (CIE 2014, w, paper 21, question 4)
The functions f and g are defined for real values of x by
\begin{eqnarray*}f(x)&=&\sqrt{x-1}-3 \mbox{ for } x>1,\\g(x)&=& \frac{x-2}{2x-3} \mbox{ for }x>2.\end{eqnarray*}
(i) Find $\D gf(37).$ [2]
(ii) Find an expression for $\D f^{-1} (x).$ [2]
(iii) Find an expression for $\D g^{-1} (x) .$ [2]
13 (CIE 2014, w, paper 23, question 7)
The functions f and g are defined for real values of x by
\begin{eqnarray*}f(x)&=& \frac{2}{x}+1 \mbox{ for }x>1,\\g(x)&=&x^2+2.\end{eqnarray*}
Find an expression for
(i) $\D f^{-1}(x),$ [2]
(ii) $\D gf(x),$ [2]
(iii) $\D fg(x).$ [2]
(iv) Show that $\D ff(x)=\frac{3x+2}{x+2}$ and solve $\D ff(x)=x.$ [4]
14 (CIE 2015, s, paper 11, question 8)
It is given that
\begin{eqnarray*}f(x)&=&3e^{2x} \mbox{ for }x\ge 0,\\g(x)&=&(x+2)^2+5 \mbox{ for } x\ge 0.\end{eqnarray*}
(i) Write down the range of f and of g. [2]
(ii) Find $\D g^{-1},$ stating its domain. [3]
(iii) Find the exact solution of $\D gf(x) = 41.$ [4]
(iv) Evaluate $\D f'(\ln 4).$ [2]
15 (CIE 2016, march, paper 12 , question 6) A function $\mathrm{f}$ is such that $\mathrm{f}(x)=6+\mathrm{e}^{4 x}$ for $x \in \mathbb{R}$.
(i) Write down the range of $\mathrm{f}$. [1]
(ii) Find $\mathrm{f}^{-1}(x)$ and state its domain and range. [4]
(iii) Find $\mathrm{f}^{\prime}(x)$. $[1]$
(iv) Hence find the exact solution of $\mathrm{f}(x)=\mathrm{f}^{\prime}(x)$. $[2]$
16 (CIE 2016, s, paper 11 , question 6) The function $\mathrm{f}$ is defined by $\mathrm{f}(x)=2-\sqrt{x+5} \quad$ for $-5 \leqslant x<0$.
(i) Write down the range of $\mathrm{f}$. [2]
(ii) Find $\mathrm{f}^{-1}(x)$ and state its domain and range. $[4]$
The function $g$ is defined by $\quad g(x)=\frac{4}{x} \quad$ for $-5 \leqslant x<-1$.
(iii) Solve $\operatorname{fg}(x)=0$. $[3]$
17 (CIE 2016, s, paper 22, question 11)
(a) A function $\mathrm{f}$ is defined, for all real $x$, by $f(x)=x-x^{2}$ Find the greatest value of $\mathrm{f}(x)$ and the value of $x$ for which this occurs.
(b) The domain of $g(x)=x-x^{2}$ is such that $g^{-1}(x)$ exists. Explain why $x \geqslant 1$ is a suitable domain for $\mathrm{g}(x)$
(c) The functions $\mathrm{h}$ and $\mathrm{k}$ are defined by h: $x \rightarrow \lg (x+2) \quad$ for $x>-2$, $\mathrm{k}: x \mapsto 5+\sqrt{x-1} \quad$ for $1<x<101$
(i) Find $\mathrm{hk}(10)$. $[21$
(ii) Find $\mathrm{k}^{-1}(x)$, stating its domain and range. $[5]$
18 (CIE 2016, w, paper 23, question 10)
The functions $\mathrm{f}$ and $\mathrm{g}$ are defined for $x>1$ by $f(x)=2+\ln x$, $g(x)=2 \mathrm{e}^{x}+3$
(i) Find $\operatorname{fg}(x)$. [1]
(ii) Find $\mathrm{ff}(x)$. [1]
(iii) Find $\mathrm{g}^{-1}(x)$. $[2]$
(iv) Solve the equation $\mathrm{f}(x)=4$. $[1]$
(v) Solve the equation $\operatorname{gf}(x)=20$. $[4]$
19 (CIE 2017, march, paper 22, question 11)
The functions $\mathrm{f}$ and $\mathrm{g}$ are defined by
$$\begin{aligned}&\mathrm{f}(x)=\frac{x^{2}-2}{x} \text { for } x \geqslant 2 \\&g(x)=\frac{x^{2}-1}{2} \text { for } x \geqslant 0\end{aligned}$$
(i) State the range of $\mathrm{g}$.
(ii) Explain why $\mathrm{fg}(1)$ does not exist.
(iii) Show that $\operatorname{gf}(x)=a x^{2}+b+\frac{c}{x^{2}}$, where $a, b$ and $c$ are constants to be found.
(iv) State the domain of gf.
(v) Show that $\mathrm{f}^{-1}(x)=\frac{x+\sqrt{x^{2}+8}}{2}$.
20 (CIE 2017, s, paper 11, question 4)
(a) It is given that $\mathrm{f}(x)=3 \mathrm{e}^{-4 x}+5$ for $x \in \mathbb{R}$.
(i) State the range of $\mathrm{f}$.
(ii) Find $\mathrm{f}^{-1}$ and state its domain.
(b) It is given that $\mathrm{g}(x)=x^{2}+5$ and $\mathrm{h}(x)=\ln x$ for $x>0$. Solve $\operatorname{hg}(x)=2$.
21 (CIE 2017, s, paper 22, question 9) A function $\mathrm{f}$ is defined, for $x \leqslant \frac{3}{2}$, by $\mathrm{f}(x)=2 x^{2}-6 x+5$.
(i) Express $\mathrm{f}(x)$ in the form $a(x-b)^{2}+c$, where $a, b$ and $c$ are constants. $[3]$
(ii) On the same axes, sketch the graphs of $y=\mathrm{f}(x)$ and $y=\mathrm{f}^{-1}(x)$, showing the geometrical relationship between them.
(iii) Using your answer from part (i), find an expression for $\mathrm{f}^{-1}(x)$, stating its domain. $[3]$
22 (CIE 2017, s, paper 22, question 12)
The function $g$ is defined, for $x>-\frac{1}{2}$, by $g(x)=\frac{3}{2 x+1}$.
(i) Show that $\mathrm{g}^{\prime}(x)$ is always negative.
(ii) Write down the range of $g$. $[1]$
The function $\mathrm{h}$ is defined, for all real $x$, by $h(x)=k x+3$, where $k$ is a constant.
(iii) Find an expression for $\operatorname{hg}(x)$. $[1]$
(iv) Given that $\operatorname{hg}(0)=5$, find the value of $k$. $[2$
(v) State the domain of hg. $[1]$
23 (CIE 2017, s, paper 23, question 9) The functions $\mathrm{f}$ and $\mathrm{g}$ are defined, for $x>1$, by $=9 \sqrt{x}$
(i) Find an expression for $\mathrm{f}^{-1}(x)$, stating its domain. $[3]$
(ii) Find the exact value of $\mathrm{fg}(7)$. $[2]$
(iii) Solve $\operatorname{gf}(x)=5 x^{2}+83 x-95$. $[4]$
24 (CIE 2017, w, paper 11, question 6)
(a) Functions $\mathrm{f}$ and $\mathrm{g}$ are such that, for $x \in \mathrm{R}$,
$$\begin{aligned}&\mathrm{f}(x)=x^{2}+3 \\&g(x)=4 x-1\end{aligned}$$
(i) State the range of $\mathrm{f}$.
(ii) Solve $\mathrm{fg}(x)=4$.
(b) $\mathrm{A}$ function $\mathrm{h}$ is such that $\mathrm{h}(x)=\frac{2 x+1}{x-4}$ for $x \in \mathrm{R}, x \neq 4$.
(i) Find $\mathrm{h}^{-1}(x)$ and state its range.
(ii) Find $\mathrm{h}^{2}(x)$, giving your answer in its simplest form.
25 (CIE 2017, w, paper 12, question 6) Functions $\mathrm{f}$ and $\mathrm{g}$ are defined, for $x>0$, by
$$\begin{aligned}&f(x)=\ln x \\&g(x)=2 x^{2}+3\end{aligned}$$
(i) Write down the range of $\mathrm{f}$.
(ii) Write down the range of $g$.
(iii) Find the exact value of $\mathrm{f}^{-1} \mathrm{~g}(4)$.
(iv) Find $g^{-1}(x)$ and state its domain.
26 (CIE 2017, w, paper 23, question 6)
The functions $\mathrm{f}$ and $\mathrm{g}$ are defined for real values of $x$ by
$$\begin{aligned}&f(x)=(x+2)^{2}+1 \\&g(x)=\frac{x-2}{2 x-1}, x \neq \frac{1}{2}\end{aligned}$$
(i) Find $\mathrm{f}^{2}(-3)$.
(ii) Show that $\mathrm{g}^{-1}(x)=\mathrm{g}(x)$.
(iii) Solve $\operatorname{gf}(x)=\frac{8}{19}$.
27 (CIE 2018, march, paper 22, question 10)
(a) The function $\mathrm{f}$ is defined by $\mathrm{f}(x)=\sqrt{1+x^{2}}$, for all real values of $x .$ The graph of $y=\mathrm{f}(x)$ is given below.
(i) Explain, with reference to the graph, why $f$ does not have an inverse. $[1]$
(ii) Find $\mathrm{f}^{2}(x)$.
(b) The function $g$ is defined, for $x>k$, by $g(x)=\sqrt{1+x^{2}}$ and $g$ has an inverse.
(i) Write down a possible value for $k$. $[1]$
(ii) Find $\mathrm{g}^{-1}(x)$. [2]
(c) The function $\mathrm{h}$ is defined, for all real values of $x$, by $h(x)=4 \mathrm{e}^{x}+2$. Sketch the graph of $y=\mathrm{h}(x)$. Hence, on the same axes, sketch the graph of $y=\mathrm{h}^{-1}(x)$. Give the coordinates of any points where your graphs meet the coordinate axes.
28 (CIE 2018 , s, paper 21 , question 5) The function $\mathrm{f}$ is defined by $\mathrm{f}(x)=\frac{1}{2 x-5}$ for $x>2.5$.
(i) Find an expression for $\mathrm{f}^{-1}(x)$. [2]
(ii) State the domain of $\mathrm{f}^{-1}(x)$. $[1]$
(iii) Find an expression for $\mathrm{f}^{2}(x)$, giving your answer in the form $\frac{a x+b}{cx+d}$, where $a, b, c$ and $d$ are integers to be found.
29 (CIE $2018, \mathrm{~s}$, paper 22 , question 10)
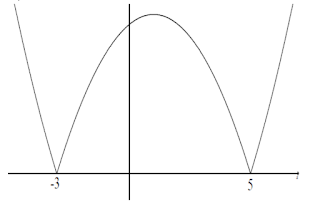
(a) (i) On the axes below, sketch the graph of $y=|(x+3)(x-5)|$ showing the coordinates of the points where the curve meets the $x$ -axis. $[2]$
(ii) Write down a suitable domain for the function $\mathrm{f}(x)=|(x+3)(x-5)|$ such that $\mathrm{f}$ has an inverse. $\quad[1]$
(b) The functions $g$ and $h$ are defined by $g(x)=3x-1$ for $x>1$, $h(x)=\dfrac 4x, x\not=0.$
(i) Find hg $(x)$.
(ii) Find (hg) $^{-1}(x)$. $[2]$
(c) Given that $\mathrm{p}(a)=b$ and that the function $\mathrm{p}$ has an inverse, write down $\mathrm{p}^{-1}(b)$. $[1]$
Answers
1.(a)(i)$\D 2(2+x)^{-3}$
(ii) $\D \frac{1-2x}{x}$
(iii) $\D x=-\frac{7}{3}$
(b) $\D gh,kg$
2. (i) $p=-40,q=-8$
(ii) $g(x)>-8$
(iii)
(iv)$\D x=e^2,x=e^6$
3.(i) $\D 0.2\le x\le 1$
(ii) $\D g^{-1}(x)=\frac{1+x}{2x}$
(iii) $\D 0.2\le x\le 1$
(iv) $x+1.25$
4(i)$\D (2x+8)^2-9$
(ii)$\D f^{-1}=\frac{\sqrt{x+9}-8}{2}$
(iii) $\D x=0.5$
5(i) 3.5 (ii) $\D h^{-1}(x)=\frac{x^2+7}{2}$
(iii) $\D x=4$ (iv) 5-4/x
6(i)1 (ii) $\D f\ge -5$
(iii) $\D 1+\sqrt{x+5}$ (v)4
7(a)(i)$\D -1\le y\le 299$
(ii) $\D x\ge 0$
(b)(i)$\D \ln\left(\frac{x+2}{4}\right)$
(ii) x=1
8(i)$\D 2^{-5}$ (ii) x=1/3,-2
9(i)3/2 (ii)4x/(3x+1)
(iii) $\D g^{-1}(x)=x^2-1$
D: $x>0$ R:$\D g^{-1}(x)>-1$
(iv)
10(i) $\D f(x)>3$
(ii) $\D f^{-1}(x)=\log_2(x+1)$
$x>3,y>2$
(iii) no solution
11(i) 3<f<7
(ii) $\D 2+\sqrt{2}$
(iii) $\D f^{-1}(x)=(x-2)^2+3$
(iv) x=19
12(i) 1/3
(ii) $\D (x+3)^2+1$
(iii)$\D \frac{3x-2}{2x-1}$
13(i)2/(x-1)
(ii) $\D gf(x)=(2/x+1)^2+2$
(iii)$\D fg(x)=2/(x^2+2)+1$
(iv) x=2
14. (i) $R_{f}: y \geq 3, R_{g}: y \geq 9$
(ii) $g^{-1}(x)=-2+\sqrt{x-5}$
D: $x \geq 9$
(iii) $x=.5 \ln (4 / 3)$ (iv) 96
15. (i) $f(x)>6$
(ii) $f^{-1}(x), \mathrm{D}: x>6$, R:real
(iii) $\ln 2$
16. (i) $2-\sqrt{5}<f(x)<2$
(ii) $f^{-1}(x)=(2-x)^{2}-5$
$\mathrm{D}: 2-\sqrt{5}<x \leq 2$
$\mathrm{R}:-5 \leq f^{-1}(x)<0$
(iii) $x=-4$
17. (a) $x=.5, y=.25$
(b) when $x \geq 1, f$ is always decreasing
(c) $1,1<k^{-1}<101$
18. (i) $\ln \left(2 e^{x}+3\right)+2$
(ii) $\ln (\ln x+2)+2$
(iii) $g^{-1}(x)=\ln \left(\frac{x-3}{2}\right)$
(iv) $7.39$ (v) $1.15$
19. (i) $g \geq-.5$
(iii) $x^{2} / 2-5 / 2+2 / x^{2}$
(iv) $x \geq 2$
(v) $f^{-1}(x)=\left(x+\sqrt{x^{2}+8}\right) / 2$
20. (ai) $f>5$
(aii) $f^{-1}(x)=-\frac{1}{4} \ln$
domain: $x>5$
(b) $1.55$ or $\sqrt{e^2-5}$
21. (i) $2(x-1.5)^2+0.5$
(ii)
(iii) $f^{-1}(x)=1.5-\sqrt{(x-0.5)/2}$
22. (i) $-6(2 x+1)^{-}$
(ii) $g>0$
(iii) $\frac{3 k}{2 x+1}+3$
$($ iv $) k=2 / 3(\mathrm{v}) x>-1 / 2$
23. (i) $x^{2} / 81+1, x>0$
(ii) $9 \sqrt{50}$
(iii) $1.6$
24. (ai) $f \geq 3$ (aii) $x=0, x=1 / 2$
(bi) $h^{-1}(x)=\frac{4 x+1}{x-2}, \neq 4$
(bii) $\frac{5 x-2}{17-2 x}$
25. (i) $y \in R$ (ii) $y>0$ (iii) $e^{35}$
(iv) $g^{-1}(x)=\sqrt{\frac{x-3}{2}}$
Domain: $x>$
26. (i) $17($ iii $) x=1,-5$
27. not $1-1$
$\sqrt{2+x^{2}}, \geq 0$
$\sqrt{x^{2}-1}$
28. (i) $\frac{5x+1}{2x}$
(ii) $x>0$
(iii) $\frac{2 x-5}{-10 x+27}$
29. (a)(i)
(aii) $x \geq 5$ or $x \leq-3$ or $-3 \leq x \leq 1$ or $1 \leq x \leq 5$
(bi) $4 /(3 x-1)$
(bii) $(4+x) /(3 x)$
(c) a










Post a Comment